Solution: Oceans Apart
Answer: SAILING/DANCING
Authors: Caroline Zhou, Darren Lee
Artists: Jamie Lai, Caroline Zhou
There are 3 parts to this puzzle (where step 1 and 2 can be done in parallel):
- Logic Puzzle
- Ship Identification
- Extraction
Logic Puzzle
This is a mashup of 2 logic puzzles (nonograms and battleships) with a twist (clued by “one-off tip” and “misinformation” in the flavortext): all of the red numbers and letters surrounding the grid are off-by-one. This means, for example, that a 2 should actually be a 1 or 3 and a B should actually be an A or C.
With this in mind, the logic puzzle can be solved by first finding the seas, then finding the ships.
Finding the Seas (Nonogram)
The letters beside (and below) the grid clue seas that are in that row (and column), similar to a typical nonogram puzzle. However, no information is given on how many cells belong to each sea, or in what order (seas are given alphabetically).
Although red seas are wrong, most of their values can be deduced immediately (without even assuming they are off-by-one) using the “contiguous region” rule. For example, row 2 must have a B, because B exists both above and below it (if row 2 didn’t contain B, then the Bs in rows 1 and 3 would be separated, and B would not form a contiguous region).
Starting with the edges of the grid, some progress can be made, but more information will be needed. As it turns out, the numbers (in range [49, 59]) next to the sea names have a sum that is equal to the sum of all the numbers inside the grid. This hints that the number next to each sea gives the sum of the numbers in that sea.
This is all the information needed to uniquely find all the seas. A more in-depth walkthrough can be found below.
Finding the Ships (Battleship)
Once the seas have been identified, we can start to find battleships. This follows standard battleship rules: the numbers beside (and above) the grid clue the number of battleship segments that are in that row (and column). (But, as mentioned above, they are off-by-one.) There is exactly one ship in each region, and like a standard battleship puzzle, ships do not touch (although, this assumption is not necessary to uniquely locate the ships).
A more in-depth walkthrough can be found below.
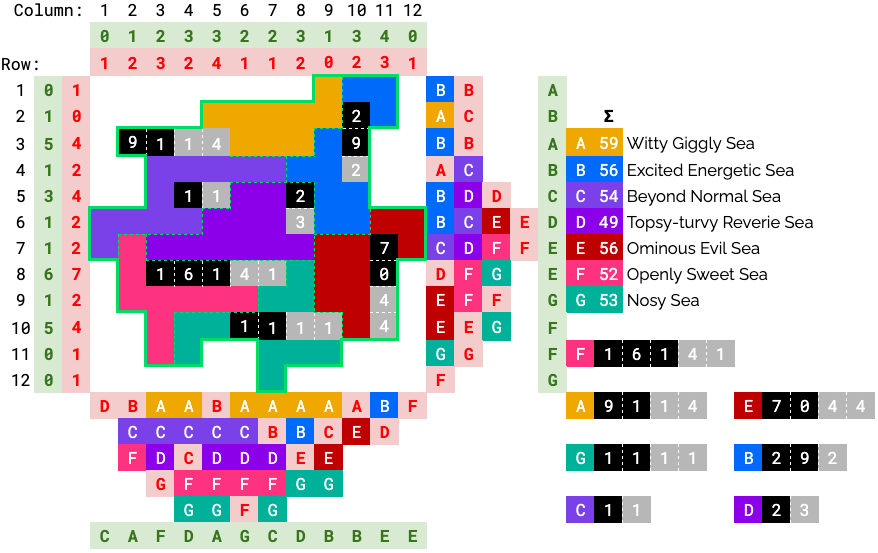
Final Grid
The completed logic puzzle should look like this, with green numbers/letters indicating the correct numbers and letters.

Ship Identification
The next part of the puzzle is to identify the 7 ships at the bottom of the page. It turns out that each ship clues a specific WEBTOON. Each ship’s name clues a WEBTOON’s title, and the sail is a specific panel from that WEBTOON.
(As a bonus: the grid’s shape and green outline resemble the WEBTOON logo, and the ships are Korean warships -- a nod to WEBTOON’s South Korean origins. These details were not necessary to notice.)
Extraction
The final part of the puzzle is to figure out what each captain is saying.
The Ep : ( )Ep : ( ) above the battleship icons hint that each battleship yields an episode number and an index (for a specific WEBTOON). The episode numbers (black) are used to help locate the panels, and the index (gray) is used to extract a letter from the speaker’s (censored) speech bubble.
But how do we match each battleship in the grid to one of the WEBTOON ships below?
At this point, we turn to the sea names, which still remain unused. The initials of the seas spell out WEBTOON GENRESWEBTOON GENRES (read 1st words down A-G, then 2nd words down A-F). Each sea’s name uses adjectives that match a specific genre (e.g. Witty Giggly = Comedy). (Also, each sea’s color matches the color used on the WEBTOON site - but this is another detail that isn’t necessary to notice.)
Each WEBTOON has a canonical genre associated with it, which can be found by visiting its webpage (or looking at its URL). (Note that on the genres page, each WEBTOON is also listed under 2 genres, but only one is used.) Use this genre to match each WEBTOON ship with a battleship to find the episode with the panel and extract a letter.
Finally, (noticing that the WEBTOON ships were given in alphabetical order by clue), take the extracted letters and order A-G to get the thematic answer to the puzzle (and an answer to how you can help these troubled captains navigate the turbulent waters): SAILINGSAILING.
| Alpha | Sea | Genre | Ship Name | Webtoon | Episode | Index | Speech | Letter |
|---|---|---|---|---|---|---|---|---|
| A | Witty Giggly | Comedy | Mighty Satanic Noble's Romantic Counsel | Love Advice from the Great Duke of Hell | 91 | 14 | I DON'T WANT TO LOSE HIM AGAIN. | S |
| B | Excited Energetic | Action | Pansophical Bibliophile | Omniscient Reader | 29 | 2 | CAN I PUNCH YOU JUST THIS ONCE? | A |
| C | Beyond Normal | Supernatural | Impure Ichor | Unholy Blood | 1 | 1 | IF I CAN'T MAKE ANY FRIENDS, I'LL JUST MAKE EVERYONE ELSE FEEL EXCLUDED INSTEAD. | I |
| D | Topsy-turvy Reverie | Fantasy | Thy Seat | Your Throne | 2 | 3 | MY LADY, YOU... ONLY LOVE HIS STATUS AND HIS THRONE! | L |
| E | Ominous Evil | Horror | Strange Stories | Tales of the Unusual | 70 | 44 | THERE ARE ALWAYS AT LEAST A FEW PEOPLE WHO’LL TRY TO BRING YOU DOWN IN LIFE.. | I |
| F | Openly Sweet | Romance | Real Allure | True Beauty | 161 | 41 | I PROBABLY LIKED HER BEFORE YOU DID! I LIKED HER SINCE HIGH SCHOOL, YOU KNOW! | N |
| G | Nosy | Drama | Pitfall with Cheddar | Cheese in the Trap | 11 | 11 | WHAT ARE YOU GONNA DO IF BORA AND I START GOING OUT? HUH?!!! | G |
Logic Walkthrough
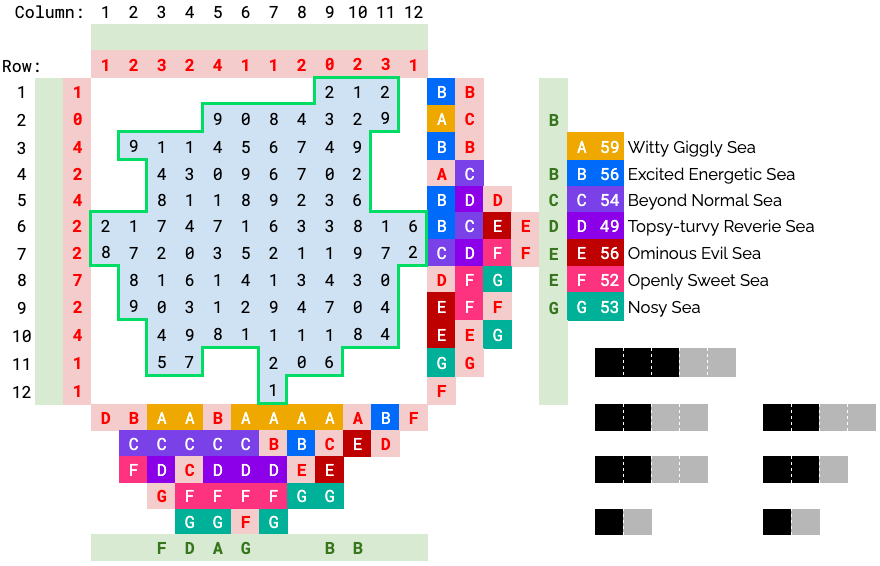
Starting with the seas, we notice that red numbers sometimes strangely collide with other seas in their row/column. If we hypothesize they might be wrong values, we can use the “contiguous regions” rule to identify many of them (by looking at what seas exist in the rows/columns around them.)
For example, row 2 must have a B since there is a B in row 1 and row 3, and we need the B’s in rows 1 and 3 to be connected.
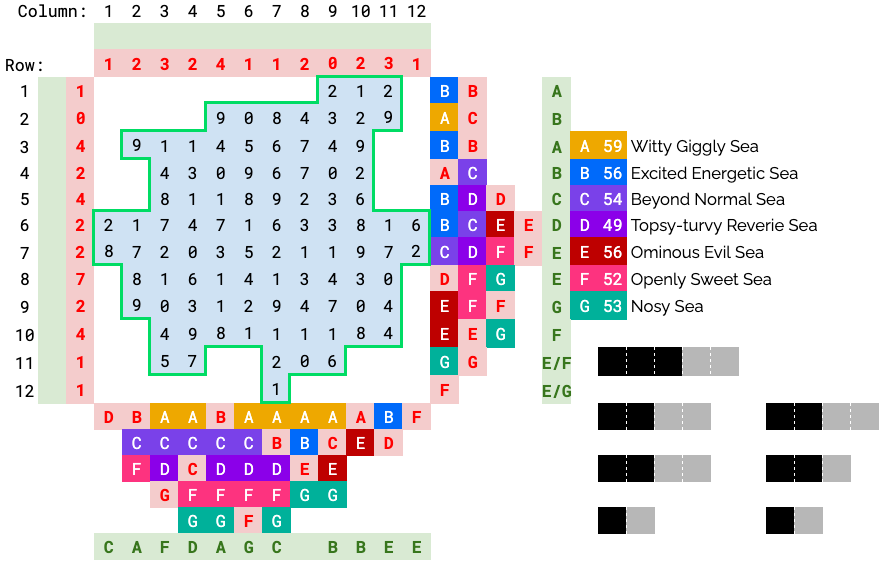
We can deduce a few more seas by looking at what they border. Row 1 must be an A since row 2 contains A and B only. We can use similar reasoning for row 10, column 11. Several others can also be narrowed down.
Row 3 must have an A, since there are As in columns 3 and 4, and A is not found in rows 4 or below.
Column 12 must be an E, since only B and E can border it, and only E exists in both rows 6 and 7. Similar reasoning can be used for column 1.
Column 7 must have a C or E by process of elimination, and must be a C since E cannot neighbor it.
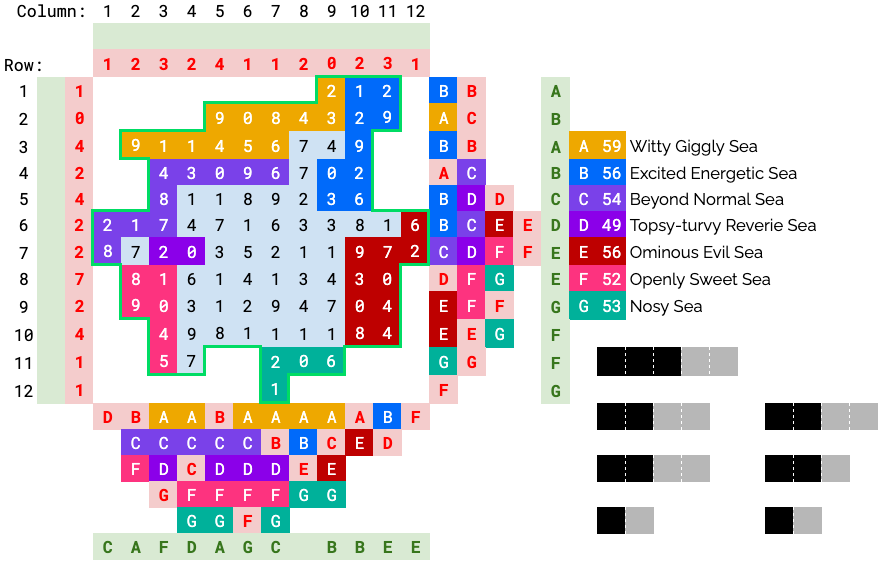
We can start filling in seas from the edges, where the number of seas is small. Cross-checking a cell’s row and column constraints place many seas uniquely along the borders.
Row 12 must be a G since column 7 doesn’t contain an E. Similarly, column 2 must be an A since row 3 must contain an A or B. Row 11 must be an F since column 3 doesn’t contain an E or G.
Cell (1, 9) must be A since the other 2 cells are already B, and row 1 needs an A. Since each sea forms a contiguous region, it must “come out” to connect to the other As and also take (2, 9) and (2, 8). Similar reasoning can be applied to C and G regions.
D must occupy (7, 3) since that’s the only cell left in column 3. It expands out to (7, 4).
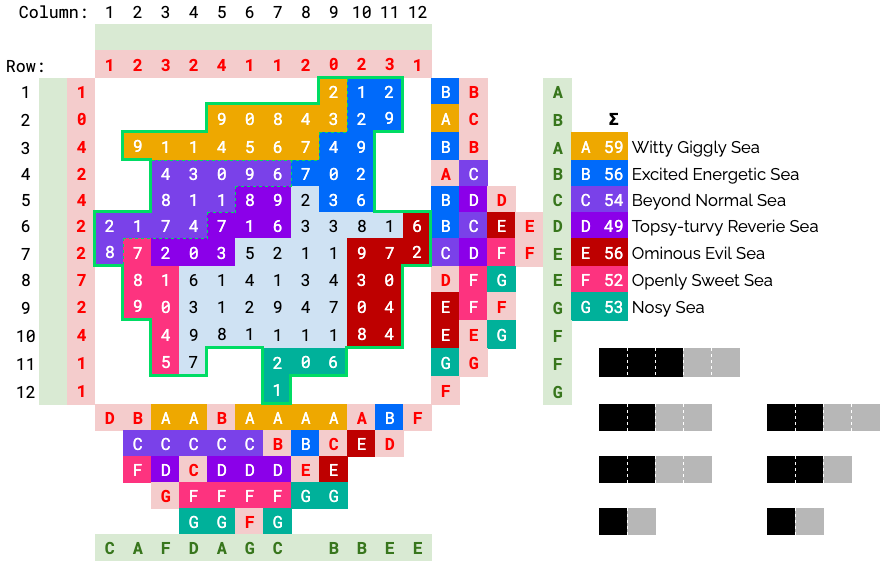
At this point, it’s hard to see how to proceed. We turn our attention to the numbers next to the sea names, and note that their sum matches the sum of the numbers in the grid.
A’s region nearly sums to 59, but is just missing the 7. This confirms the hypothesis, and allows us to complete sea A.
Similarly, C is only missing 6 more, and can’t take any of the large 7-9 neighboring cells, so it takes (5, 4), (5, 5), and (6, 4), completing its sum.
B, D, and F expand to take remaining cells next to A and C.
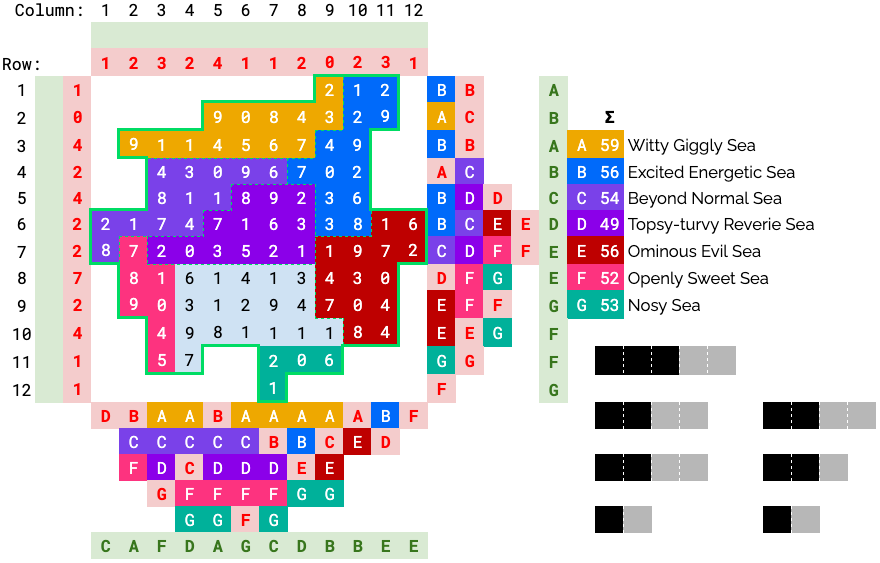
B is missing 11, so considering the remaining cells it can control, it must take the 8 at (6, 10).
Similarly, E must take the 7 at (9, 9) and 4 at (8, 9) to fill its missing 13 quota. (Note it can’t expand to column 8).
Since B and E each can only take in 3 more for their sums, only D can take (6, 8), and now all the wrong letters are resolved.
Considering the bounds of D, it must take the remaining cells in its box to fill its remaining sum. Sea D is now complete.
This also lets us finish sea B, which must take the 3 at (6, 9), and sea E, which must take the 1s at (6, 11) and (7, 9) (which no other sea can reach now).
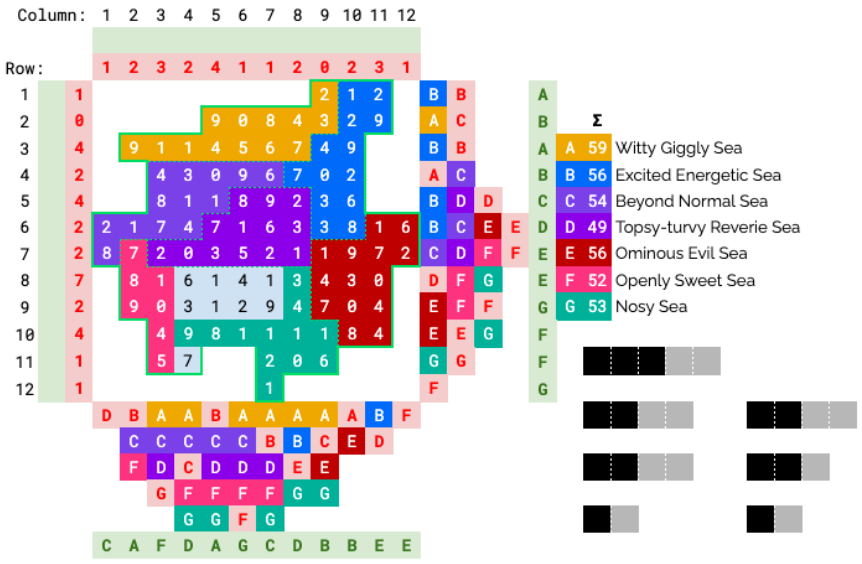
This leaves F and G to resolve. G takes the remaining cells in columns 8 and 9, since F isn’t found there.
F currently sums to 34, and needs 18 more to get to 52. Now consider the 9 at (10, 4). If F takes this, it must also take the 7 at (11, 4), since G would not be able to reach this. But then, F has nowhere left to expand because all the neighboring numbers are too large.
So the 9 at (10, 4) must belong to G, as well as the rest of row 10 (otherwise F would cut off G).
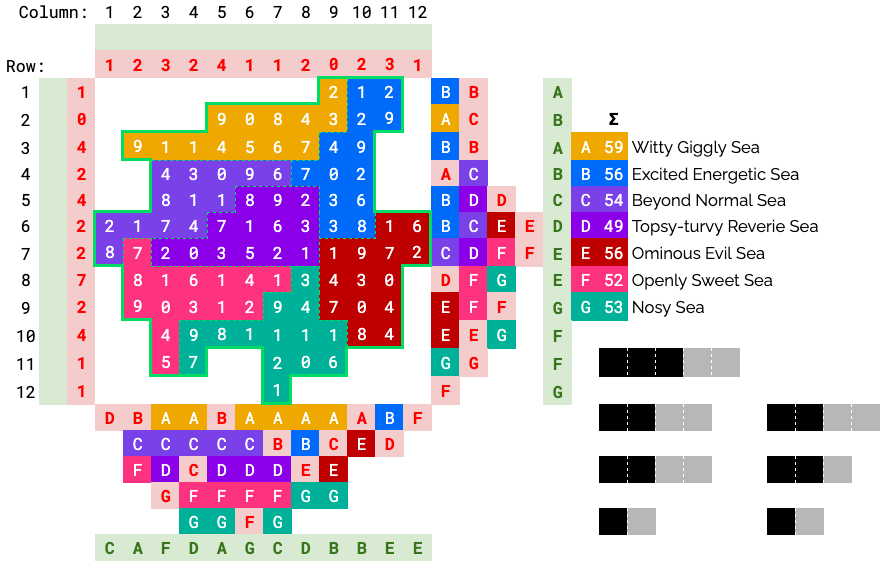
Almost there! Note that F is found in columns 4-7, so must stretch out to either (8, 7) or (9, 7) (or both). Consider the 9 at (9, 7). If F takes this, the only path back that doesn’t exceed the sum is to take the rest of row 9… but then there is no way to sum to 3 using the remaining numbers.
So, the 9 at (9, 7) must belong to G and the 1 at (8, 7) must belong to F.
The only way to complete G (which needs 7 more) without cutting off F is to take the 7 at (11, 4). F takes the remaining cells and the seas are now fully resolved.
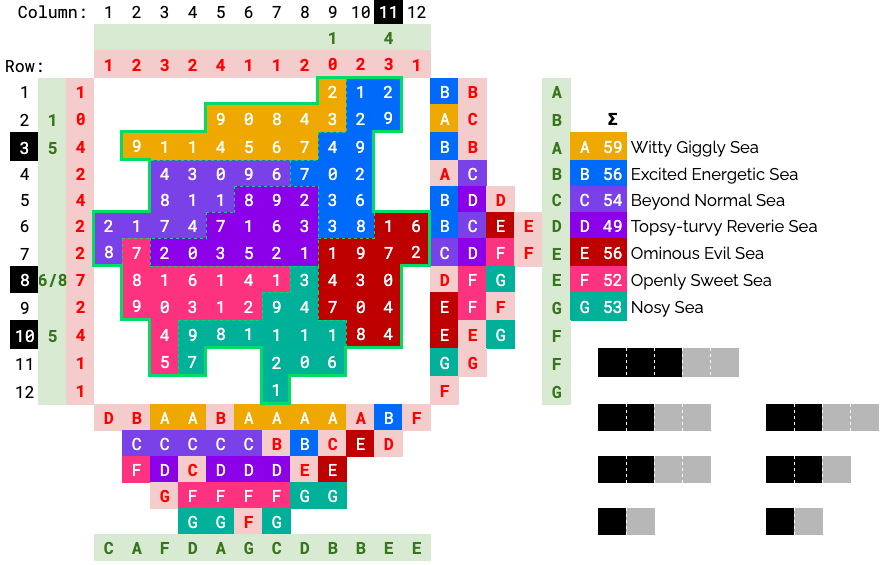
We can now consider the battleships. Since the numbers are also red (like the wrong letters), we also hypothesize these are wrong. (Also, their sums do not match the number of segments, so something is definitely wrong.)
Taking this one step further, we may realize that they should all be off-by-one, as the seas also are, and the flavortext says “one-off.”
As a freebie, all 0’s can be marked as 1’s (since we can’t have negative segments).
We can start by considering where the 4 4+ length ships can go. For a 4+ length ship to exist, the clue must be >= 3, and there must be enough room in a sea to fit a 4+ length ship.
The candidates are columns 3 and 11, and rows 3, 8, and 10. However, Column 3 cannot contain a length 4 ship since if it did, row 8 can’t be satisfied (at least 6 segments must be found, but the rest of pink cannot hold segments if its ship is vertical in column 3. There are only 4 cells left in that row, so this is not possible).
There now remain only 4 candidates so each one must hold a length 4+ ship, and we can fix most of the clues accordingly. (We mark these candidates black here.)
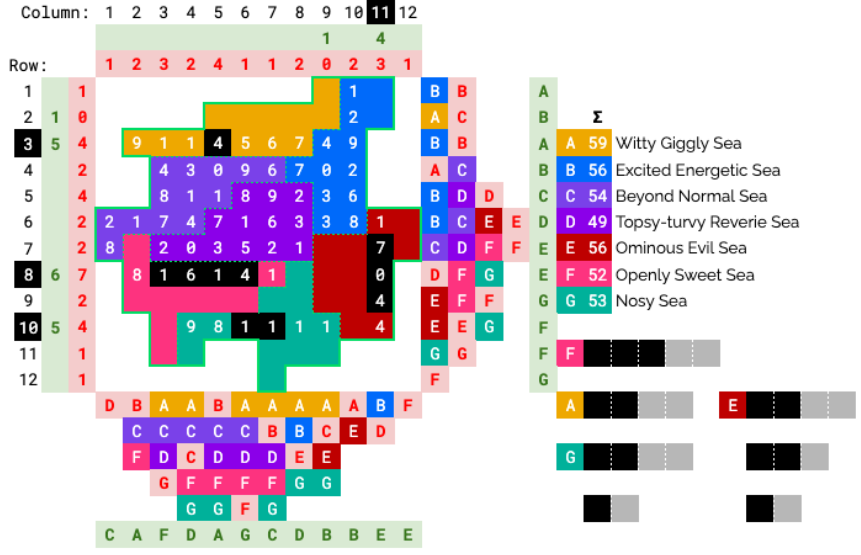
We now see that the 4 4+ length ships must go in A, E, F, and G. All other cells in those seas must then be unoccupied (rules state each sea contains exactly 1 battleship).
By removing these cells, we see that row 8 must contain the 5 length ship in order to reach 6. So, the other 3 candidates must hold the 4 length ships.
We can mark cells that must contain parts of these ships.
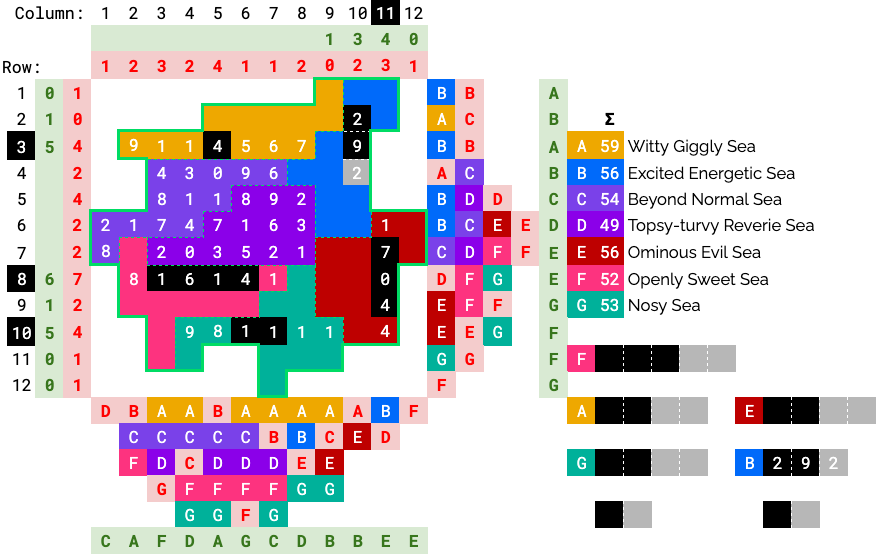
We can now correct more of the clues.
Notably, row 2 must contain a segment, and it must be in B at (2, 10). This ship must go vertically in column 10, so the rest of the cells in B are unoccupied.
Since the clue for column 10 is 2, it must be a 1 or 3. It can’t be a 1, so it must be a 3, and so the length 3 ship must be in B. Further, it cannot occupy row 1, since there’s no way to fit 2 segments in row 1, so row 1 contains 0 segments.
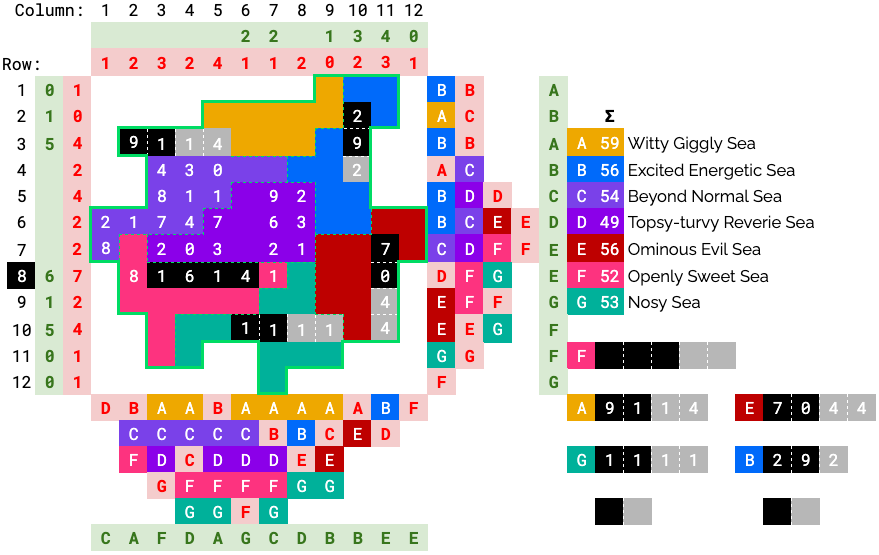
The ship in G can be fully resolved since column 9 dictates 1 segment, and no other cells can be occupied now.
Column 6 is finished, too. That leaves only one place for the A ship to go.
Furthermore, the ship in E extends downward to satisfy row 10’s clue.
All the length 4 ships are now found.
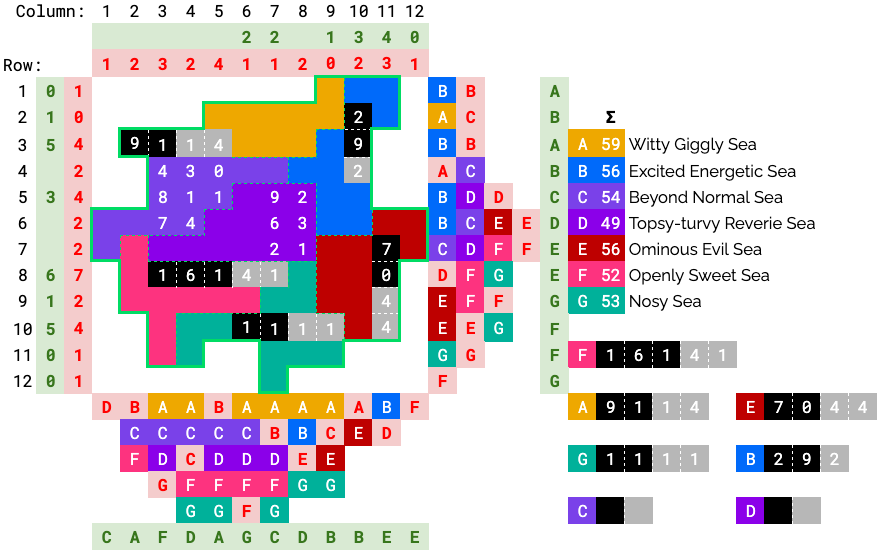
We now turn our attention to seas C and D, which need to contain the 2 2 length ships.
Note that row 5 says there must be either 3 or 5 segments in that row, and only C and D are now involved. Since both ships have length 2, 5 segments is not possible. To satisfy 3 segments, both ships must touch this row. So every cell in that is not adjacent to row 5 cannot contain a ship.
This also lets us finish F’s ship: column 2 can no longer contain 3 segments, so it contains 1 segment, which is taken by A. F’s ship extends east.
Sin Extraction
For the sin extraction, notice that in each sea, all digits 0-9 appear except for one digit (excluding the numbers that the ship covers).
Take these numbers and index into the speaking characters' names in A-G order. Some character names can be easily found in wikis. Some others are a little harder to find but usually their names will also be mentioned elsewhere in the episode.
| Alpha | Character | Missing Number | Extraction |
|---|---|---|---|
| A | Dantalian | 1 | D |
| B | Dokja | 5 | A |
| C | Hayan | 5 | N |
| D | Psyche | 4 | C |
| E | Yaeji | 5 | I |
| F | Seojun | 6 | N |
| G | Younggon | 5 | G |
Authors’ Notes
- This puzzle was inspired by Caroline’s love for WEBTOONs. She has a long list of recommendations for anyone who may be interested. We hope people enjoyed scanning through some of the WEBTOONs and might be interested in reading more after doing this puzzle. :)
- All the characters are shown in states when they’re displaying some form of Envy, to thematically tie into the sin extraction. This thematic framing also spurred our idea to do a “lying” logic puzzle, where people might spread misinformation to others out of envy. Coincidentally, episode numbers are often also “off-by-one” from their # (e.g. for Cheese in the Trap, episode 1 is #2 in the series… this is because WEBTOONs often include a prologue, which is episode 0.)
- Originally, all 93 episodes of Unholy Blood were publically available, but after we started writing the puzzle, it went to Daily Pass (meaning only the first 12 episodes are free, and to see more, you need to download the App), so we had to use an early episode. Despite the possibility of people brute forcing it by scanning all the public episodes, we liked the WEBTOON enough to keep it. (Plus, we see it as a plus if people are reading through it :)).
- In addition to the WEBTOONs referenced in this puzzle, Caroline also recommends: